Delta T Cheese Vat Cook Temperature Profile Control System
The Delta T cheese vat cook control was developed to control the temperature during the cooking step to match a desired temperature cook profile. Generally, the temperature during the cooking step is increased from the current temperature to a final temperature in a specific length of time. A steady increase in temperature is needed to achieve good curd contraction and expulsion of whey. Poor temperature control during the cooking step will have adverse effects on yield and curd quality.
A typical PID loop does not work well controlling temperature with a continuously increasing set point. PID loops work well for maintaining a temperature set point in a steady-state process and can handle upsets to steady state or single steps in the set point. Trying to control to a constantly increasing set point stretches the ability of a PID control loop. The result could be a constant offset from set point, or with aggressive tuning, cycling may occur. There is also a long lag time in temperature response, which can cause PID tuning difficulty. One situation to avoid would be having the temperature increase too quickly, which could decrease curd quality and yield.
The Delta T cheese vat cook control was developed to control the temperature during the cooking step to match a desired temperature cook profile. Generally, the temperature during the cooking step is increased from the current temperature to a final temperature in a specific length of time. A steady increase in temperature is needed to achieve good curd contraction and expulsion of whey. Poor temperature control during the cooking step will have adverse effects on yield and curd quality.
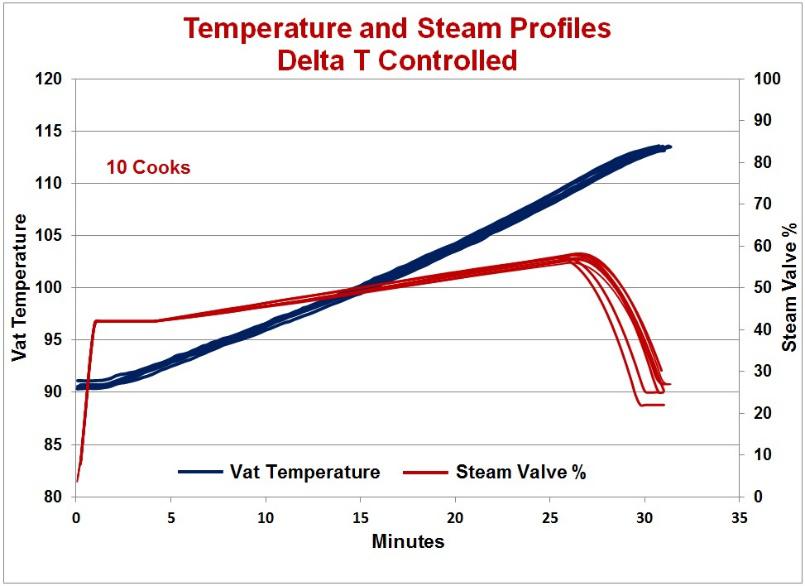
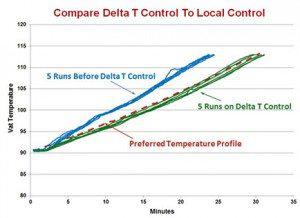
The Delta T system uses a model of the temperature profile and focuses on controlling the rate of temperature increase instead of controlling to a temperature set point. This control method avoids the situation of the temperature rising too quickly as it is controlling the temperature rate of change. The system uses the current or starting temperature, the final temperature, the cook minutes, and a profile factor to calculate the temperature profile. The profile factor determines the degree of ‘curve’ in the temperature profile. The profile curve can be straight line or degrees of concave or convex. The concave curve would have a constant increasing rate of temperature change and the convex would have a constant decrease in the temperature rate of change. The cheese type and agitation would dictate which profile to use. One chart below shows examples of calculated temperature profiles. Several options are available, such as the controlling the agitation speed based on temperature. The other chart compares the actual vat temperatures during the cooking steps of ten batches, five before Delta T control and five with Delta T control. As seen in the chart, the Delta T controlled temperature followed the desired profile to the final temperature and in the right amount of time.

Graph showing 10 random cooking curves. Notice all ten curves are stacked, thus demonstrating the precision in control of cooking curves (Read Article).